题解 P11506
题意
一个表格有 $n$ 行,无限多列,在每一列中要求行数为 $k$ 的倍数的格子里有 $x$ 个数,其他各自中有 $y$ 个数,格子中的数按照自然数顺序排序。共 $q$ 次询问,求给出的数 $a_1, a_2, \dots, a_q$ 在表格中的行数。
下图是一种 $n = 7$, $k = 3$, $x = 2$, $y = 3$ 的情况,同题面样例:
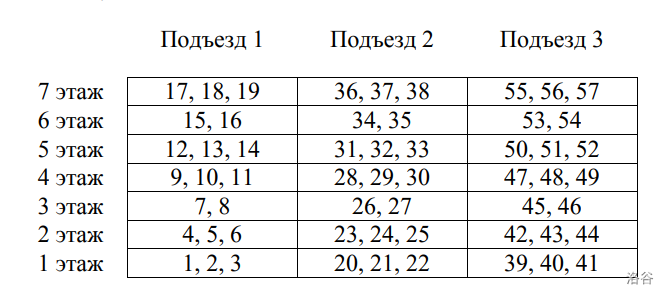
思路
如果对于每一次询问,直接按照题意模拟填数的话,时间复杂度为 $\text{O} (qn)$ ,显然只能通过 subtask #1 。
考虑优化,规定每填 $k - 1$ 次 $y$ 和 $1$ 次 $x$ 为一个周期。
我们可以预处理出每一列填入数字的数量和一个完整周期内填入数字的数量 $S_T$ 和 $S_k$ ,如果 $a_i > S_T$ , 那么 $a_i$ 所在的行数与 ${a_i}^{\prime} = a_i \bmod S_T $ (${a_i}^{\prime} < S_T$) 所在的行数相同,可以缩小一定范围的常数。
接下来对于每次询问 ${a_i}^{\prime}$ ,我们可以计算出其经历了几个完整的周期,以及周期之外最后剩余的行数。这些都可以通过数学方法直接处理,时间复杂度 $\text{O} (q)$ 。
-
在周期之内,计算经历了几个完整的周期,直接用 ${a_i}^{\prime}$ 整除 $S_k$ 即可。这一部分答案为周期数乘以周期 $k$ 。
-
在周期以外,因为每个周期前 $k-1$ 格均为 $y$ 情况,最后 $1$ 格为 $x$ 情况,我们先判断其是否在周期的最后 $1$ 行,如果是,这一部分答案即为周期 $k$ 。反之则前面每一格内数量均为 $y$ ,使用周期外数字的数量除以 $y$ ,判断一下是否整除即可。
以样例为例, $S_T = 8$,$S_k = 19$ ,若询问 $a_1 = 50$ ,那么 ${a_1}^{\prime} = a_1 \bmod n = 12$ , ${a_1}^{\prime}$ 经历了 $1$ 个完整的周期,最终剩余 $2$ 行,所以最终答案为 $3 + 2 = 5$ 。
核心判断语句如下:
1 | ll query(ll a){ |
代码
评测记录:https://www.luogu.com.cn/record/197131297
代码(C++):https://www.luogu.com/paste/0ulbm2nd
闲话
很好的签到题,注意 $a_i \leq 10^{18}$ 要开 long long 。



